相関係数って？

二つの変数間の関連の強さを表す指標です。

例えば、身長という変数と体重という変数は、一般的に、身長が高いひとほど体重が大きいといえます。 この2つの変数の関連の強さを指標化したものが相関係数です。

公式の意味を分析したものを備忘録として記事にしました。

相関係数の公式の考え方

相関係数の公式は下記の通りです。

 

 

 

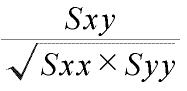
簡単に説明すると、

• 分子=変数間の相関関係を出力する部分
• 分母=単位を調整する部分

を指しています。 分子と分母に分けて、内容を分析してみましょう。

変数間の相関関係を出力する分子

まずは単位を気にせず、「身長が大きい人は体重も大きいよね」ということを分子で示しましょう。

仮にAさんからZさんまでの人がいるとします。 最初に、AさんからZさんまでの身長と体重を計測し、平均値を算出しておきます。

平均値を出すのは、「身長が大きいかどうか」を判断するための比較対象として、平均と比較して差分を出すためです。 （ちなみに、この平均と実際の値の差を偏差と呼びます） さて、実際にAさんについて見てみましょう。

Aさんの身長の偏差：（Aさんの身長181-平均値171）=10

同じく、体重でも平均と比較して差分を出します。

Aさんの体重の偏差：（Aさんの体重80-平均値65）=15

Aさんの身長と体重の偏差を掛けあわせます（偏差積）

Aさんの身長と体重の偏差積：10×15=150

これで、Aさんの身長と体重の偏差積が150とでました。 これをZさんまで繰り返して、全ての偏差積を足し合わせます。（=偏差積和=共分散） この共分散が大きくなるか、小さくなるかで関連性を図るのが相関係数の考え方です。 つまり、ざっくりいうと、

• 偏差積和がプラスになると、正の相関
• 偏差積和が0に近くなると、無相関
• 偏差積和がマイナスになると、逆相関

という考え方。 実は、下記の相関係数の公式における分子が表しているのが、この共分散（偏差積和）なのです。

 

 

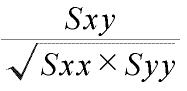
以上より、分子は下記の説明が可能です（全て同じ意味です）

• XとYの共分散
• XとYの偏差積和
• ある標本において、xの値からxの平均値を引く。同様に、yの値からyの平均値を引く。それらを掛けあわせる。それを全標本で行い、全て足したもの

以上が、関連の大きさを表す分子の分析です。 このままでは、単位やデータの数によって結果を比較できないので、それを調整するために分母に数式を入れます。

単位を調整する役割の分母

次に、分子で表した関連の大きさの単位を調整する分母の分析です。 分子である偏差積和は、

• Xの平均からの差（=Xの偏差）と、
• Yの平均からの差（Yの偏差）を
• 掛けあわせて
• 全部足したもの

でした。 つまり、

• Xの平均からの差の和と
• Yの平均からの差の和の
• 掛けあわせ

に対応する調整要因があります。 以上を踏まえ、

1. Xの偏差平方和の根と
2. Yの偏差平方和の根を
3. 掛けあわせる

という考え方で調整します。 （※偏差平方和とは、各変数における、平均からの距離を合計したものです）

 

 

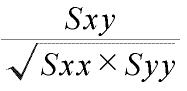
あらためて、公式の分母をみると、

• Xの偏差平方和の根（√Sxx）と
• Yの偏差平方和の根（√Syy）を
• 掛けあわせている

のがわかると思います。 以上、相関係数の公式の分析は終了です。 参考にした書籍等をあげておきますね。